Система координат (Альфiйська)

Альфíйська систéма координа́т - система координат, яка була розроблена гравцем AlPhAE у вересні 2019, і є загальноприйнятою на сервері. Складається з широти, довготи і висоти, подібно загальноприйнятій в реальному світі системі координат.

Широта

Широта́ - координатна вісь, що збігається з координатною віссю z в грі. На відміну від осі z, альфiйська система координат зумовлює спосіб вимірювання широти таким чином, що її значення не перевищують 0.01*z. Дана формула сприяє полегшеному взаємодії гравця з координатами світу, допомагаючи йому уникати тисячні і мільйонні значення. Таким чином,

$\Phi ~=~{\frac {Z_{og}}{100}}$

де Ф - широта, Z - координати осi z.

Дана інтерпретація широти не може бути цілим числом, так як в протилежному випадку, приведення значення широти до цілого числа могло б сильно вплинути на точність вимірювання координати, особливо, якщо координата по z приймає мільйонні значення.

Наведемо приклад. Припустимо, ви побудували будинок на координаті -1500 по z. Тоді, значення його широти буде Ф = -1500/100 = -15,00.

Таким чином, межа світу в 30 000 001,5 блоків матиме значення широти Ф = 300 000,015 на пiвночi і стільки ж на пiвднi. Наявність сторін світа в грі дозволяє розділити широту на північну і пiвденну, тобто абревіатура пн. ш. буде використовуватися, якщо Ф приймає від'ємні значення, а пд.ш. - якщо позитивні. Це також дозволяє зробити вибір - або використовувати мінус, або використовувати тільки позитивні значення, при цьому вказуючи пн. ш. і пд.ш.

Довгота

Довгота́ - координатна вісь, що збігається з координатною віссю x в грi. Так само, як і широта, відрізняється від значень осі x в 0.01 раз, тобто для неї також справедлива наступна формула:

$\Lambda ~=~{\frac {X_{og}}{100}}$

де $\Lambda$ - довгота, X - координати осi x.

Також, як і широта, має дві інтерпретації - або знакова (мінус, плюс), або абревіатури з.д.(якщо має знак мінус), с. д.(якщо має позитивні значення).

Висота

Висота́ - координатна вісь, що збігається з координатною віссю y в грi. Так само, як і широта, і довгота, відрізняється від значень осі y в 0.01 раз, тобто для неї також справедлива наступна формула:

$\mathrm {H} ~=~{\frac {Y_{og}}{100}}$

де $\mathrm {H}$ - висота, Y - координати осi y.

Однак, на відміну від широти і довготи, в інтерпретаціях не має відсилань до реального світу, тому як і мінус-плюс, значення висоти можуть бути доповнені абревіатурами н.а. (нижче адмiнiмуму(якщо значення висоти негативні)) , в.а. (вище адмiнiмуму(якщо значення висоти позитивні)).

Функціональний аналіз системи

Так як простежується залежність широти, довготи і висоти від координат, значить в деякому просторі функцій однозначно визначені 3 функції:

$f(z)~=~0.01~\times ~z$
$g(x)~=~0.01~\times ~x$
$h(y)~=~0.01~\times ~y$

На основі даних функцій можна скласти графіки, щоб простежити поведінку цих функцій і поведінку функцій, якi зумовлюють значення X,Y,Z. Розглянемо на прикладі першої функції.

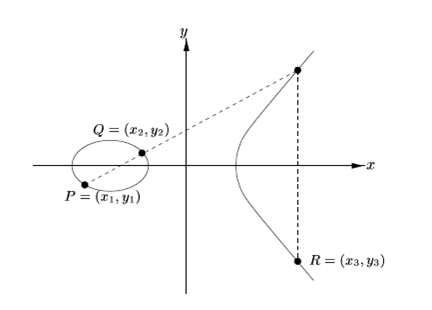
Функція $f(z)$ є монотонно зростаючою, так як вона зростає на всій області визначення, тобто

$\forall m,k\in \mathbb {R} :m<k\rightarrow f(x_{m})<f(x_{k})$

Функція є непарною і аперiодичною, так як не існує такого числа Т, при якому було б справедливо

$\forall T\neq 0\rightarrow f(z+T)=f(z)$

але справедливо

$f(-z)=-f(z)$

Так як областю визначення функції є відрізок $E=[-30000001.5;30000001.5]$, то справедливо говорити, що

$\sup f(z)\approx 300000$
$\inf f(z)\approx -300000$

або

$\lim _{z\to \sup E}f(z)=\sup f(z)$

А тепер розберемося з прирощенням функції $f(z)$. Так як функція монотонна і зростає, то її приріст на всій області значень буде позитивним. Що щодо диференціала функції, який є лінійною частиною приросту функції, то в деякій точці $x_{0}$ він буде дорівнює

$\mathrm {d} _{x_{0}}f(z)=f'(x_{0})z$

де $f'(x_{0})$ позначає похідну $f$ в точці $x_{0}$, а z -приріст аргументу при переході від $x_{0}$ к $x_{0}+z$. Таким чином, підставляючи значення, отримаємо

$\mathrm {d} f(z)=(0.01\times z)'=0.01$

Це означає, що диференціали вихідної функції $f(z)=z$ і функції $f(z)=0.01z$ відрізняються також в 100 разів або в 0.01:

$\mathrm {d} f(z)=z'=1$

Таким чином, знайдені $\sup f(z),\inf f(z),\lim f(z),\mathrm {d} f(z)$ для функції $f(z)=0.01\times z$ відрізняються від цих же значень вихідної функції $f(z)=z$ в 0.01 раз, а значить справедливо вважати, що функція відрізняється від вихідної в 0.01 рази.

Загальні відомості

Альфійська система координат ефективно організовує звичайну систему координат в грі, що дозволяє працювати з більш великими значеннями. Однак, це призводить і до ряду незручностей, а саме - разом із зростанням значень X,Y,Z, ростуть і дробові частини широти, довготи і висоти, що призводить до більш кропіткої роботи з математичними обчисленнями даних осей, так як доводиться працювати з дробовими частинами, довжина яких іноді може досягати 10 і навіть 20 символів.